Ten artykuł jest skróconą, przetłumaczoną na potrzeby OpenTTD wersją tego artykułu z angielskiej Wikipedii
Geometria taksówkarska, także metoda manhattańska - sposób obliczania odległości, stosowany w OpenTTD.
Zasada działania
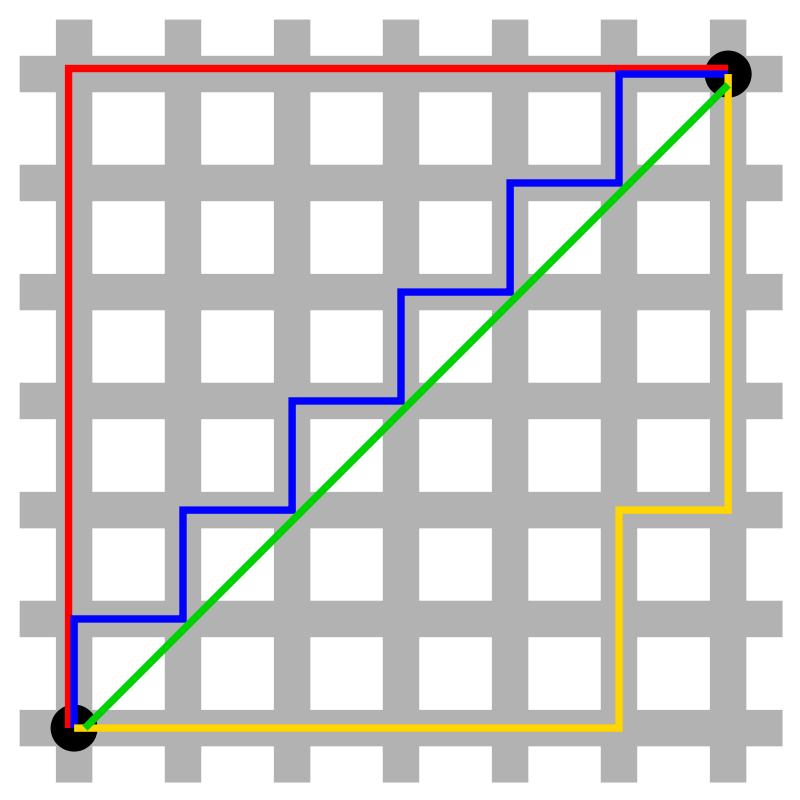
Metoda ta przypomina metodę stosowaną do pomiaru odległości przez taksówkarzy na nowojorskim Manhattanie - od tego pochodzi jej nazwa. Zasada działania opiera się na prostokątnym układzie ulic Nowego Jorku (czy też kratek, w przypadku OpenTTD). Na rysunku po prawej zieloną linią zaznaczono najkrótszą odległość między dwoma punktami. Linie: czerwona, niebieska i żółta, to pomiar metodą manhattańską - "po kratkach" (zwróć uwagę, że długość tych trzech linii jest równa (wynosi 12), a linia zielona jest (zawsze ok. 1,4 raza) krótsza).
W praktyce
Na ilustracji poniżej, pociąg wozi drewno z lasu do tartaku:
- Linią białą oznaczono najkrótszą trasę pomiędzy tymi przedsiębiorstwami. Trasa ta ma długość około 24 kratek.
- Linia błękitna pokazuje trasę, którą pokonuje pociąg. Jej długość to około 29 kratek.
- Czerwona linia wyznacza jedną z możliwych tras wyznaczoną metodą manhattańską. Trasa ma długość 34, i właśnie taka długość będzie używana do obliczeń w grze (na przykład - zobacz: Przychód z ładunku, Mechanika gry: Przychód za ładunek)
Jak wspomniano na początku, zawsze istnieje więcej niż jeden sposób pomiaru odległości metodą manhattańską. Na rysunku poniżej przedstawiono przykładowe inne sposoby (zwróć uwagę, że żółta, pomarańczowa, czerwona i wiśniowa linia mają tę samą długość):
Wskazówki
Jak można zauważyć na powyższych ilustracjach, w przypadku transportu na skos (nierównolegle do linii pól w grze), odległość jaką pokonuje pojazd jest mniejsza niż ta wykorzystywana do obliczeń (mierzona metodą manhattańską). Z tego powodu transport na skos daje większe zyski.