Postępy: 95%
- Pomóż rozbudowywać poprzez pomoc w tłumaczeniu.
- Przeczytaj Instrukcję Stylów przed edycją.
- Pamiętaj, aby usunąć ten szablon, gdy artykuł zostanie przetłumaczony w całości.
- Sygnalizacja · Stacje · Skrzyżowania · Budowa składu · Projektowanie lini & Triki
Linie tramwajowe · Żegluga · Lotnictwo · Modyfikacja terenu
Contents |
Pojemność (nośność) twoich sieci transportowych
Ta strona ma być opisem teoretycznych przykładów pozwalających zwiększyć przepustowość określonej sieci transportu lądowego.Oczywiście o wiele ważniejsze będzie rozmieszczenie węzłów i rozplanowanie przebiegu sieci lecz jej przepustowość też ma duże znaczenie.
Rozstaw semaforów (SD)
Jest to dość oczywiste. Im dalej od siebie ustawione są sygnalizatory tym mniejsza jest przepustowość trakcji wynikająca z przeciętnej prędkości pociągów na objętych sygnalizacją odcinkach. Z wartością SD (signal distance} wynoszącą jeden sygnał na każde N kafli, minimalny odstęp pomiędzy dwoma pociągami jadącymi z pełną prędkością nie może być mniejszy niż N+1 (rys.1). Na torze po przekątnej jeden sygnał co 2N "pół kafli" lub N „pełnych kafli” minimalna przerwa nie może być mniejsza niż 2N+1 "pół kafli" lub N+1/2 "pełne kafle". Gdy pociągi są tak blisko siebie , osiągasz teoretycznie maximum pojemności danej trakcji co w praktyce jest raczej niemożliwe.
Jedną z ważnych kwestii jest konsekwencja. Pojemność ścieżki zależy od tego, która przerwa sygnału jest największa. W związku z tym ścieżka z jednym sygnałem na każde dwa kafle, która ma anomalną, jednorazową przerwę wynoszącą trzy lub cztery kafle, będzie miała znacznie zmniejszoną pojemność i może potencjalnie zacinać się i naruszać zasadę 1 (Rysunek 2). Pamiętaj, że dotyczy to również narożników i podziałów/połączeń.
Diagonal track
W OpenTTD, pociągi poruszają się wolniej na zakręcie (thanks SmatZ!), i dlatego wymagają zwiększonej gęstości sygnału, aby zapobiec wąskim gardłom. Ważne jest, aby odstęp między pociągami (a nie SD) torów prostych i ukośnych był jak najbardziej zbliżony. W przeciwnym razie pociągi mogą się zacinać podczas jazdy z prostej na ukośną lub z ukośnej na prostą.
Szybki eksperyment wykazał, że w tym samym czasie pociąg porusza się o 2 pola po prostym torze, równie szybki pociąg porusza się po około 3 "pół kafli" po torze ukośnym. Więc jeśli używasz pewnych ustawień autosygnałów, prawdopodobnie będziesz musiał ręcznie zwiększyć gęstość sygnału na dowolnej kątowej szynie, którą posiadasz.
Poniższe przykłady zostały stworzone przy założeniu, że długość pociągu zmienia się również na torze ukośnym. Wydaje się, że dotyczy to tylko niektórych NewGRFów! (Iirc, to prawda dla JapanSet i źle dla domyślnych pociągów.)
- Ustawienie autosygnału na 3 daje minimalny odstęp między pociągami równy 4. To przekłada się na minimalny przekątny odstęp między pociągami wynoszący 6 "połówek kafli", co można uzyskać umieszczając sygnały w odległości 5 "pół kafli" (lub dwukrotnie umieszczając sygnały z autosygnałem ustawionym na 5).
- Ustawienie autosygnału na 2 daje minimalny odstęp między pociągami wynoszący 3. To przekłada się na minimalny przekątny odstęp między pociągami wynoszący 4,5 "pół kafli". Przekątną przerwę między pociągami wynoszącą 5 "połówek kafli" można uzyskać, umieszczając sygnały w odległości 4 "pół kafli" lub ustawiając autosygnał na około 2. Przekątną przerwę między pociągami wynoszącą 4 "połówki kafli" można uzyskać umieszczając sygnały z odległością 3 "pół kafli" (lub poprzez dwukrotne umieszczenie sygnałów z ustawieniem autosygnału na 3). Chociaż to SD' nie ma dokładnego odpowiednika na torze ukośnym, odchylenie między torem prostym i ukośnym wynosi tylko 1/3 pola, a to samo ustawienie autosygnału może być użyte dla toru prostego i ukośnego.
- Ustawienie autosygnału równe 1 daje minimalny odstęp między pociągami równy 2. Przekłada się to na minimalny przekątny odstęp między pociągami wynoszący 3 "pół-kafli", co można osiągnąć umieszczając sygnały w odległości 2 "pół kafli" lub za pomocą automatycznego ustawienie 1. Tutaj to samo ustawienie autosygnału jest używane również dla toru prostego i ukośnego.
Więc jakiej odległości sygnału powinienem użyć?
-
Dwa kafle
Wartość SD równa dwóm daje minimalny odstęp wynoszący 3 i jest optymalnym praktycznym rozwiązaniem. Nie uwzględniając wariantu kosztów .
-
Jeden kafel
SD z jednego jest pełen problemów. Nawet podział ścieżki powoduje lukę sygnalizacyjną. Byłoby możliwe łączenie kątowych szyn z przerwą sygnałową 1, ale spowodowałoby to znaczny wzrost złożoności konstrukcji.
-
Połówka kafla
Ścieżka pod kątem może przesyłać sygnały o podwójnej gęstości. Może to być interesujące teoretycznie lub w celu skrócenia o kilka milimetrów sytuacji, która może się wydarzyć. Największą wadą w przypadku połowy kafla SD jest oczywiście to, że każdy prosty kawałek toru będzie miał większe SD.
Cokolwiek wybierzesz SD , pamiętaj, że musisz być konsekwentny. Sieć z wartością SD równą 2 i przerwą sygnalizacyjną równą 3 na często używanej ścieżce może prowadzić do zacięć. Dlatego może mieć mniejszą pojemność niż sieć o stałym poziomie SD wynoszącym 3!
Długość pociągu (TL)
To jest miecz obosieczny. Dłuższy pociąg zwiększy prawdopodobieństwo poniesienia realistycznej kary za przyspieszenie, sprawiając, że konstrukcja będzie bardziej rozłożona i złożona. Jednak dłuższy 'TL zwiększa maksymalną ładowność twojej sieci. Zwróć uwagę, że w przypadku silników, które mają sekcję przednią i tylną, dodatkowe 1/2 pola zajęte sprawia, że krótsze pociągi są jeszcze mniej korzystne.
W przypadku sieci o dużej szybkości typowe wartości od trzech do pięciu pól są normalne, przy czym cztery są szczególnie preferowane, ponieważ na torze o wartości SD wynoszącej 2 linie TL-4 pociągi przyspieszanie z postoju ma krótszy czas reakcji niż pociągi z nierównym TL .
Obliczanie nośności
Gęstość pociągu (TD)
Twoja sieć będzie obsługiwać określoną liczbę pociągów i zakładając, że masz znormalizowaną długość pociągu, możemy zdefiniować pewne metryki. Wartość Gęstość pociągów (TD) dla toru jest podawana w jednostkach pociągów na tysiąc kafli i można ją obliczyć, zliczając liczbę pociągów na tym torze i dzieląc ją przez długość toru.
Typowe zmierzone wartości dla niezoptymalizowanej sieci 4-polowych pociągów to TD wynoszący 25 (pociągów na 1000 pól).
Maksymalną wartość TD , zanim korki zaczną się samoczynnie rozprzestrzeniać, można zmierzyć, zezwalając kolejce pociągów na przyspieszenie od zatrzymania, a następnie mierząc odległość pociąg-pociąg, gdy wszystkie pociągi osiągną pełną prędkość, i używając wzoru
1000 / (TL + train gap)
Ten krytyczny TD zależy od mocy i liczby silników, masy pociągu, maksymalnej prędkości, SD i długości pociągu. Ponieważ ta krytyczna gęstość obejmuje informacje o przyspieszeniu i czasie osiągnięcia maksymalnej prędkości, może również informować o praktycznej maksymalnej przepustowości sieci. Na przykład korzystanie z pociągów o niższej prędkości maksymalnej w rzeczywistości ułatwia posiadanie gęstej sieci. Przeciętny odstęp między pociągami jest znacznie mniejszy w przypadku kolei niż w przypadku kolei jednoszynowej lub maglev. Wolny nie oznacza jednak lepszego, ponieważ zmniejszona gęstość linii zostanie z nawiązką zrekompensowana krótkimi czasami realizacji.
Na przykład, w pełni naładowana 4-kafel Chimaera (top-end MagLev (en)) ma odległość pociąg-pociąg równa 12, co daje gęstość krytyczną 1000/16 lub 62,5. Powtarzając poprzedni przykład, ale przy użyciu szyny elektrycznej T.I.M. Podaje odległość pociąg-pociąg wynoszącą tylko 6 i gęstość krytyczną równą 100.
Możliwe jest uruchomienie sieci z gęstością wyższą niż krytyczna, ale jest to niewskazane.
Teoretyczna maksymalna gęstość pociągu
Mówiąc najprościej, jest to gęstość pociągów, jeśli twoja sieć jest całkowicie wypełniona pociągami w minimalnej odległości między sobą. Nigdy tego nie osiągniesz.
Jest to podane przez 1000 / (TL + SD + 1)
Na przykład pociągi składające się z 4-kafli i odległość sygnału 2 dadzą teoretyczną maksymalną gęstość pociągu równą 140.
Nośność (CC)
Ponieważ TL zmienia nośność linii, porównywanie TD z różnymi TL jest bez znaczenia. Aby porównać wskaźniki efektywności między różnymi osobistymi preferencjami, potrzebujemy nowej miary. Ta nowa miara będzie po prostu miarą tego, ile jednostek ładunku w Twojej sieci transportuje rocznie na torze. Będzie wprost proporcjonalna do średniej ilości ładunku na kafel toru, a także do szybkości, z jaką ten ładunek się porusza.
CC_day = TC / ( TL + TD ) * v_travel CC_day = TC / ( TL + TD ) * v_kmh * 74*2/16/256*1.00584 CC_day = TC / ( TL + TD ) * v_mph * 74*2/16/256/1.6
CC_day = carrying capacity ładowność [w jednostkach ładunkowych dziennie] to ile ładunku może przejechać każdy kafel w ciągu jednego dnia. Taka ilość ładunku może być dostarczona na początek linii i dostarczona na koniec linii.
TC = train capacity pojemność pociągu [w jednostkach cargo], ile ładunku może przewieźć jeden pociąg.
v_travel = prędkość [w kaflach/dzień], v_kmh = prędkość [w km/h] i v_mph = prędkość [w mil/h] to prędkość pociągu.
TG = train gap przerwa kolejowa [w kaflach]. W przypadku układów torów, które nie powodują 'wstrzykiwania' pociągów do strumienia-o-dużej-gęstości, jest to krytyczna luka w pociągach.
TL = trainlength długość pociągu [w 'kaflach'].
Chimaera z powyższego przykładu ma nośność
CC_day=47*6*402/16*0,0056=40 Passengers/day lub CC_day=27*6*402/16*0,0056=23 Worków kosztowności/dzień
T.I.M. Z powyższego przykładu ma nośność
CC_day=40*6*150/10*0,0056=20 Pasażerów/dzień lub CC_day=20*6*150/10*0,0056=10 Bags of Valuables/day
Prace nad tym urządzeniem są w toku.
Zwiększenie wydajności sieci
Ok, więc teraz, gdy zdefiniowaliśmy parametry, które już intuicyjnie zrozumieliśmy, jak możemy ich użyć do ulepszenia naszych sieci? Złota zasada numer 1 optymalizacji sieci mówi, że pociągi w sieci nigdy nie zwalniają. Istnieją dwie możliwe części sieci, w których może się to zdarzyć, podzielenia i łączenia.
Rozdzielenia
W przypadku podziału toru należy upewnić się, że w punkcie podziału nie ma dłuższej-niż-normalna luki sygnalizacyjnej. Można temu zaradzić poprzez ostrożną lub nadmierną sygnalizację.
Łączenia
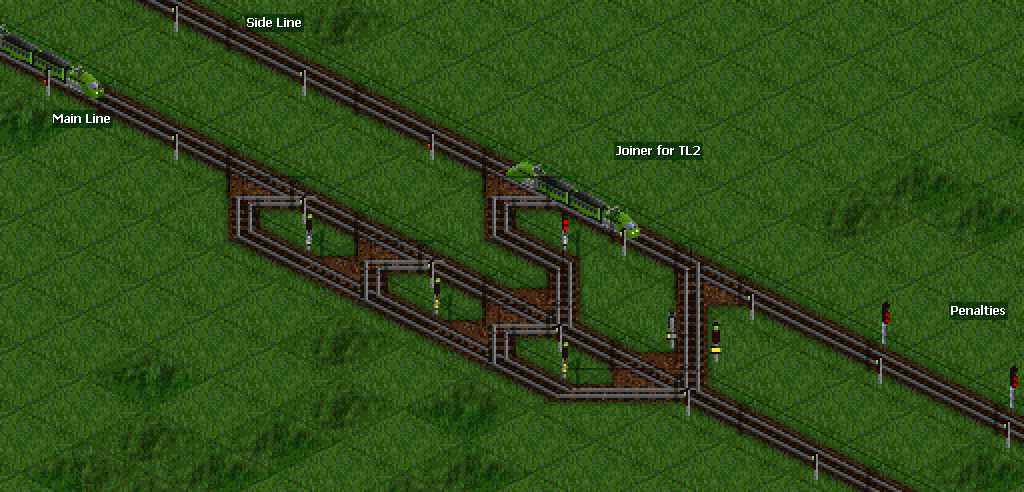
Łączenia się stanowią dla nas wyjątkowy problem. W przypadku trywialnego połączenia pociągi na głównej linii mogą zostać potencjalnie zatrzymane przez pociąg boczny. Jest już zbiór prac na temat Priorities autorstwa naszych kolegów z obwodu kooperacyjnego. Lektura tego linku powinna zapoznać Cię z zasadami scalania priorytetowego.
Rozważ typowe połączenie bez skrzyżowań przy wyjściu ze stacji odbioru. Na stację wjeżdża ciasno upakowany, zoptymalizowany strumień pociągów, ale z powodu różnic w czasach załadunku kolejność ta jest zakłócana na wyjściu ze stacji i kończy się na dwóch torach luźno upakowanych pociągów. Jedna z tych linii, oznaczona jako główna, będzie miała średnio luki między pociągami wystarczająco duże, aby zmieścić trzeci pociąg. Proste połączenie dwóch linii nie zadziała i wymagane jest scalenie według priorytetów.
Należy odnotować, że ponieważ pociągi zrzucające ładunek zawsze spędzają ten sam czas na peronie, możliwe jest zdematerializowanie i ponowne złożenie ciasno upakowanego strumienia pociągów, nawet powyżej krytycznej gęstości! (Rycina 3)
Połączenie z pierwszym-przejściem z wykorzystaniem bloku priorytetowego zmniejszy współczynnik ruchu z 1: 1 do około 3: 1 na korzyść toru głównego (rysunek 4). Dodanie połączenia o drugim priorytecie bezpośrednio po pierwszym byłoby daremnym gestem, ponieważ pociągi na obu liniach kontynuowałyby jazdę z tą samą prędkością, a pociąg główny po prostu ponownie domagałby się pierwszeństwa. Wprowadzenie opóźnienia w postaci pętli toru, po którym nastąpi połączenie z drugim priorytetem, zredukuje linię boczną do zwykłej strużki pociągów i wypełni większość dostępnych miejsc na głównej linii. Istniejące rozwiązania wymagałyby wstępnego przyspieszenia, jednak cyklotron eliminuje potrzebę utraty pędu.
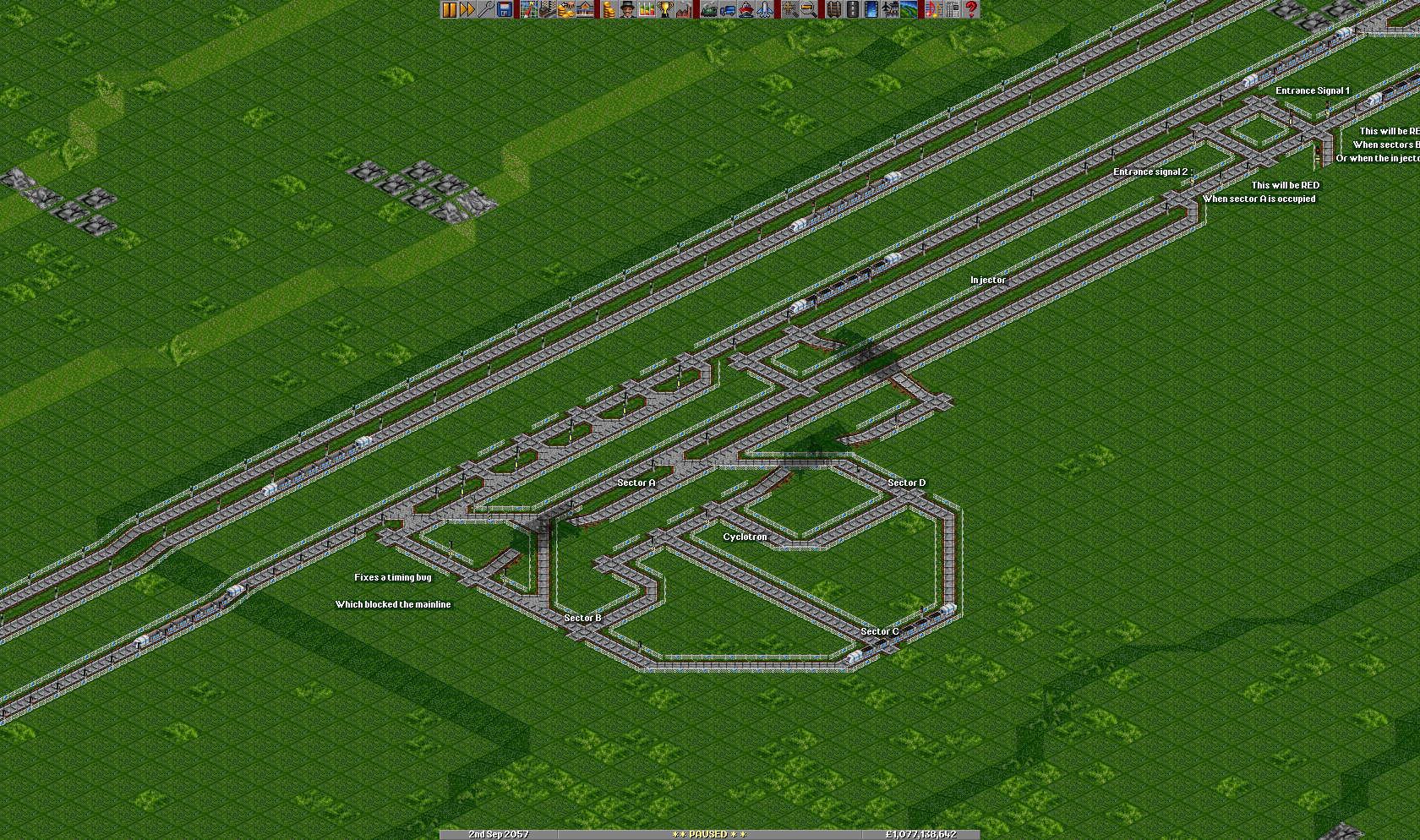
Cyklotrony
Rozważ kwestię poboczną, która zapętla się z powrotem po nieudanym scaleniu priorytetów. Pociąg w tej pętli kontynuowałby ponowne testowanie głównej linii pod kątem warunków wejścia, co 8 * 'TL kafli, aż znalazłby wystarczająco dużo miejsca, aby połączyć się z główną linią. Po opróżnieniu cyklotronu następny czekający pociąg mógł wstępnie przyspieszyć i zostać 'wstrzyknięty' do cyklotronu, gotowy do kontynuowania cyklu. Ten system ma jednak pewne wady, ponieważ ma pojemność jednego pociągu i będzie wiele straconych okazji, ponieważ pociąg jest w niewłaściwej pozycji na akceleratorze. [Usunięto uszkodzony link do Simple Cyclotron.] Skrzyżowania to duży i dobrze wydeptany obszar otwartego toru; Ograniczyłem się do nierozgałęzionych struktur podajników. Przekonasz się, że wysoce zoptymalizowany strumień pociągów NIE znosi dobrze skrzyżowania.
Możliwe są udoskonalenia cyklotronu. Na pętli torowej jest wystarczająco dużo miejsca, aby pomieścić dwa pociągi, a system sygnałów priorytetowych umożliwi opcjonalne wejście drugiego pociągu do cyklotronu. Przy dwóch pociągach w cyklotronie będzie podwójna szansa na wejście do slotu na głównej linii. Aby zapobiec korkom drogowym wewnątrz cyklotronu (co byłoby katastrofalne), konieczne są pewne poprawki opóźnienia, ale wynik końcowy jest niezwykle przydatny.
Opóźnienie wtrysku zakłada, że drugi wtryskiwany ciąg przyspiesza od zatrzymania, i istnieje niewielka szansa, że drugi pociąg faktycznie trafił na wejście cyklotronu z pełną prędkością. W takim przypadku czas będzie nieprawidłowy i drugi pociąg prawie na pewno spowoduje zator w cyklotronie (a tym samym na głównej linii). Można to zrekompensować dodatkową sygnalizacją w celu odfiltrowania pociągów o pełnej prędkości. Odfiltrowane pociągi o pełnej prędkości mogą zostać skierowane do drugiej pętli lub po prostu pozbawione pędu przez sygnał.
Cyklotron zawierający wszystkie omówione optymalizacje i kilka dodatkowych poprawek pokazano na rysunku 5.
[Usunięto uszkodzony link do stanu gry.]
Nota redaktora: Chociaż chciałbym bronić moich udoskonaleń cyklotronu, eksperymenty dowiodły, że przyspieszenie wstępne jest solidniejszym systemem. Te dwa elementy zostały połączone w wcześniej połączonym zapisie gry.
☑
☑
☑
☑
☑
☑
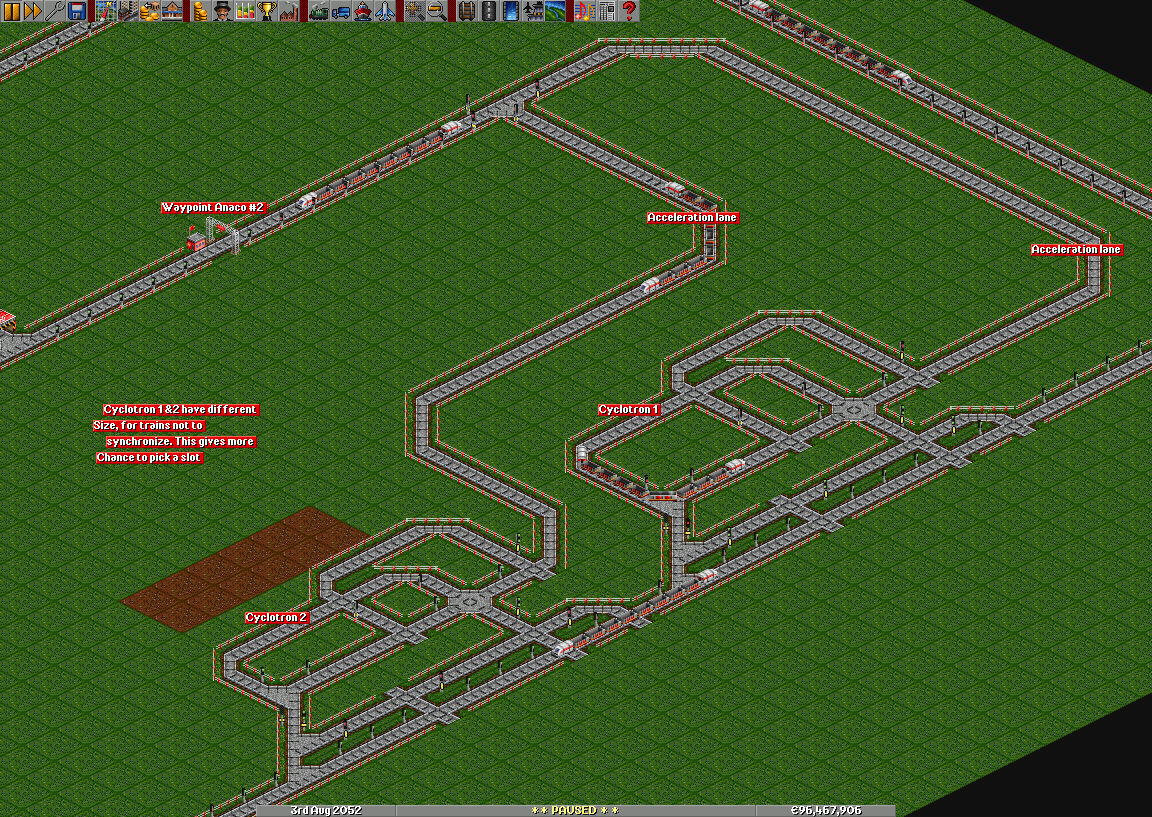
Cyklotrony równoległe
Próba zminimalizowania wad w pełni funkcjonalnego cyklotronu prowadzi do równoległych, małych, jednosegmentowych cyklotronów. W tej konstrukcji szereg cyklotronów, z których każdy obsługuje jeden pociąg, może być zasilany jednocześnie. Mogą mieć różne rozmiary pętli, aby zapobiec synchronizacji między pociągami rowerowymi, dając większe szanse na znalezienie szczeliny w przepływie głównej linii. Każda pętla nadal potrzebuje własnego pasa przyspieszenia, więc pociągi wjeżdżają na nią z pełną prędkością. Gdyby zdarzyło się, że pociąg wjechał na pętlę z małą prędkością, miałby szansę wjechać na główną linię z prędkością inną niż maksymalna i spowodować prawdopodobnie duży korek uliczny.
Rysunek 6 przedstawia równoległy cyklotron z dwiema pętlami.
Zapisana gra z przykładem podanym na rysunku 6 jest dostępna Here (jeden z plików GRF użytych w tej grze nie jest obecnie dostępny do pobrania) (wersja 0.7 lub wyższa wymagana do otwarcia).
Zalety w stosunku do w pełni funkcjonalnego cyklotronu:
- Może obsługiwać więcej niż dwa pociągi
- Szybsze tempo niepowodzenia i ponowienia
- Nie ma potrzeby synchronizacji zapętlonych pociągów
- Łatwiejszy do zbudowania i zapamiętania
Wady:
- Większy przy użyciu więcej niż jednej pętli